Takeaways from my Functional Programming Course
Cornell's CS 3110
I took CS 3110 this past semester (Fall 2017) and I was enlightened. I had not been a programming enthusiast all these years, and (anticlimactic), still not am. However, I learned a great deal about Functional Programming (FP) and was extensively impressed by its offerings. Some basic definitions for terms in this post:
-
Imperative Programming: A programming paradigm that uses statements that change a program’s state (Wikipedia). In other words, a paradigm where the control flow involves statements like
int x = 3;ory = "string"etc. and procedures/methods rule the world with side-effects during computation. Python will be the major example reflecting this paradigm in this post. -
Functional Programming (FP): A style that treats computation as the evaluation of mathematical functions and avoids changing-state and mutable data (Wikipedia). In other words, statements are non-existent, and functions are treated as values. Definitions/declarations like
let x = 3do not change the state of the world. OCaml will reflect this paradigm in this post.


While lambda calculus, which I would go as far as to call the basis of FP, has been around for more than 70 years
More selfishly and importantly, FP concepts have aided my understanding and coding style immensely, and I will share some of those concepts in this post. Obviously, I won’t make justice in doing so, and I will provide other resources in the end of the post to start or advance in this study. I think of FP as a combination of two paradigms: computational representation of formal mathematical arguments and immutability. I will encorporate the former in discussing higher-order functions and type-inference. Since the latter could be a separate post in itself, I’ll not go in extreme depth of understanding immutable values in FP. I won’t discuss the benefits or differences of FP and imperative programming because that would be an uninteresting and fruitless discussion.
OCaml's top-level
Remember Python's interactive interpreter? It provides a simple terminal-based interface to test and program Python. If you have Python installed on your machine, and you know how to start the interactive interpreter that comes with it, then the Python VM can act as a nifty computer for programming. OCaml developers provide a similar top-level or utop where you can interactively play with OCaml.
I'll use Python's interactive interpreter and OCaml's utop for most examples in this post. You can also use this online resource to do OCaml.
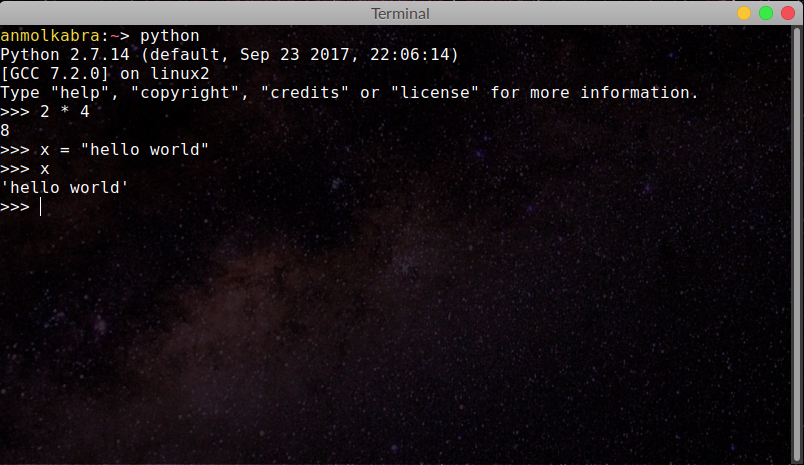
An Introduction to Immutability
It’s ironical that we are discussing immutability when all classical computers are founded on mutable values and computation. Those Intel or AMD CPU chips only house a limited number of registers (memory units) to perform all required computations. Therefore, the chips must erase and rewrite registers with updated values to perform a new computation. These classical computers, which are based-off of the Von Neumann architecture new and delete operators, and C also requires programmers to manage memory in the heap (malloc and free). But FP works on a higher-level of abstraction and allows you to not worry a lot about these low-level details.
I like this idea. Read it again: people needn’t care about memory management and can only ponder on the algorithms and computation. The internet overflows with posts about why functional programming is superior because of this advantage, and Prof. John Hughes of Glasgow University, U.K., even wrote a paper on a similar topic
Where or Why Immutability is Good in Programming?
Many proponents of immutability argue that immutable values are easy to deal in multi-threaded programs x, must be updated in a program. A single-threaded program wouldn’t cause worrisome behavior, but a multi-threaded program would cause havoc.
.
.
.
# precondition: len(data) >= 3
>>> data[1] = data[0]
>>> data[2] = data[1]
In an list/array of length 3 or more and in a single-threaded run, this code would update data[1] and data[2] to values data[0] and data[1] respectively, where the second change would occur after the first one has completed. However, multiple threads trying to run this code might update values incorrectly. In an array [1, 2, 3, 4], a single-threaded program would expectedly update the array to [1, 1, 1, 4]. Whereas, a multi-threaded program could update the array to [1, 1, 2, 4] by updating data[2] before updating data[1] and thus committing an unforgivable sin. Such are the grave dangers in programming with mutable data values that immutability diligently avoids.
However, most FP languages don’t provide syntactic structures to deal with single elements of the list. OCaml only allows access to the head and tail of the list. To get the nth element of the list, you would have to recurse down the list and obtain that nth head of the sub-list; you can also let the library function List.nth do the recursion for you. More importantly, OCaml won’t easily allow you to mutate the values of lists.
(* defining a list is easy *)
# let lst = [1; 2; 3; 4];;
val lst : int list = [1; 2; 3; 4]
(* accessing a list's elements *)
# let head_elt = List.hd lst;;
val head_elt : int = 1
# let tail_lst = List.tl lst;;
val tail_lst : int list = [2; 3; 4]
# let snd_elt = List.nth 1 lst;;
val snd_elt : int = 2
When you’re not allowed to mutate values, there is no way threads will be allowed to do so (given your language is implemented by reasonably-minded developers). Sure it comes with disadvantages, particularly when the program has memory constraints. However, when the computer could do memory management and garbage collection for you and/or memory capacity is abundant, why worry about memory allocation/deallocation? Immutability may not be an extremely game-changing idea, but I like that it tends to draw my focus to algorithms, away from low-level memory management.
Immutability in Imperative Languages
This is a challenge, and I can’t think of a way to achieve this to a satisfactorily level. This is partly due to the Von Neumann architecture foundations and partly because imperative languages are riddled with mutable data structures and variables. Even so, I prefer to avoid using the same variable name repeatedly and mishaps such as the one in the previous section. One could also embody immutability by conscious choice and just not intentionally update or mutate data values. Just create new ones and use them, and let Java and Python runtime VMs collect garbage! Memory is cheap at the moment, and gone is the age when 1 GB of RAM cost you a fortune.
Even so, immutability is hard when your language allows mutability.
Classism in Functions
This is my favorite takeaway. An absolute gem. FP is not classist per se, but FP embodies the idea of mathematical formulation of programs by considering functions as values (the concept of considering functions as values also requires the notion of closures, but this will do). Just as you would pass around \(f(x) = x^2\) in expressions like \(f' + f = 0\), FP lets you pass around functions. Because functions (closures to be precise) are values, they can take functions as arguments and also produce functions as results. This is also supported in many imperative languages like Python or Java, but the notion is different. I believe that functions can be passed as arguments in Python since they are treated as objects and vice-versa. I don’t know about Java, but I believe in Java to contain such a game-changing feature. So there are 2 notions in this classification of functions:
- functions taking functions, and
- functions returning functions
Functions Taking Functions
This is quite easy to do in OCaml, and similar implemntations are possible in most FP languages:
# let double = fun x -> 2 * x;;
val double : int -> int = <fun>
# let modify_int = fun f -> fun x -> f x;;
val modify_int : ('a -> 'b) -> 'a -> 'b
(* 'a, 'b are briefly discussed later;
they are not the focus here *)
# modify_int double 4;;
- : int = 8
In the above code snippet, double is a simple function that takes an integer x and returns the double of x. double’s syntax is also easy to understand: fun x -> 2 * x is the part of code line doing the job, and double is taking all the credit. modify_int is the higher-order function in this example, taking in the double function and an integer 4, and applying double to 4. modify_int’s definition is similar to that of double, but the noticeable distinction is that modify_int takes in a function f and then a value x and applies f to x. All this is good, but one could have just typed double 4 in utop and got 8 as the result. Functions taking functions can be of great use when you don’t have to define double at all:
...
# modify_int (fun x -> 2 * x) 4;;
- : int = 8
Here we just don’t give the credit of doubling to a named function double and let the hard-working anonymous function fun x -> 2 * x do its job and take the credit.
One could program similar instances in many imperative languages as well. Here’s one in Python:
>>> def double(x):
... return 2 * x
...
>>> def modify_int(f, x):
... return f(x)
...
>>> modify_int(double, 4)
8
And the one with an anonymous function to avoid writing double in Python at all:
>>> modify_int(lambda x: 2 * x, 4)
8
Wait, did I write lambda to define an anonymous function in Python? Another instance where imperative languages draw heavily from lambda calculus.
Functions Returning Functions
In OCaml
These types of functions are commonplace in OCaml because the language supports partial application. This means that a function can be applied to some of its inputs and not all, returning a function that could input the rest of the inputs. There is an obvious restriction that the arguments listed in order must be used before those that come later in the argument list. For example, modify_int can be partially applied to double or the anonymous function variant to obtain a function that doubles:
# modify_int double;;
- : int -> int = <fun>
# modify_int (fun x -> 2 * x);;
- : int -> int = <fun>
(* we can also program double as *)
# let double' = modify_int (fun x -> 2 * x);;
val double' : int -> int = <fun>
How is this idea useful? Let’s say you want to apply a function to the first element of a list but would like to write many such functions.
A naive approach is to do this:
(* precondition: List.length lst >= 1 *)
# let double_fst = fun lst -> 2 * (List.hd lst)::List.tl lst;; (* :: is the prepend or cons operation *)
val double_fst : int list -> int list = <fun>
# let triple_fst = fun lst -> 3 * (List.hd lst)::List.tl lst;;
val triple_fst : int list -> int list = <fun>
A novice approach is this:
(* precondition: List.length lst >= 1 *)
# let nble_fst = fun n -> fun lst -> n * (List.hd lst)::List.tl lst;;
val nble_fst : int -> int list -> int list = <fun>
# let double_fst = nble_fst 2;;
val double_fst : int list -> int list = <fun>
# let triple_fst = nble_fst 3;;
val triple_fst : int list -> int list = <fun>
And a legendary approach is this:
(* precondition: List.length lst >= 1 *)
# let modify_fst = fun f -> fun lst -> f (List.hd lst)::List.tl lst;;
val modify_fst : ('a -> 'a) -> 'a list -> 'a list = <fun>
# let nble_fst = fun n -> modify_fst (fun hd -> n * hd);;
val nble_fst : int -> int list -> int list = <fun>
# let double_fst = nble_fst 2;;
val double_fst : int list -> int list = <fun>
# let triple_fst = nble_fst 3;;
val triple_fst : int list -> int list = <fun>
The novice approach is more concise and less code-repetitive than the naive one. Why do I say that the last approach is legendary even when it is more lines-of-code than the novice? Think how much code you would have to write in the novice approach if you were to write a function that added n to List.hd lst. We have nble_fst in the novice approach to multiple n to List.hd lst, but we would have to write a similar addn_fst that adds n to List.hd lst. The legendary approach will be more concise when it comes to this. By using higher-order functions that take-in and return functions, we have abstracted the verbose implementation in modify_fst and can get any function that modifies the first element by passing the corresponding function to modify_fst. Truly legendary.
In Python
Python doesn’t aid programmers to build functions that return functions easily. This is primarily because Python doesn’t support partial application of functions. Although it’s achievable, the code is more verbose due to Python’s syntactic styles.
# precondition: len(lst) >= 1
>>> def modify_fst(f, lst):
... # apply f to lst[0], and concat the two lists, [hd] and tl
... return [ f(lst[0]) ] + lst[1:]
...
>>> def nble_fst(n):
... # trying something similar to the OCaml version
... return modify_lst(lambda hd: n * hd)
...
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: modify_fst() takes exactly 2 arguments (1 given)
# Python can often be painful. It doesn't support partial application.
>>> def nble_fst(n):
... def nble_fst_helper(lst):
... return modify_fst(lambda hd: n * hd, lst)
... return nble_fst_helper
...
>>> double_fst = nble_fst(2)
>>> double_fst( [1, 2, 3] )
[2, 2, 3]
>>> triple_fst = nble_fst(3)
Concluding ‘Classism in Functions’
Higher-order functions enable programmers to think enormously more but code tremendously less. I know we don’t need so many adverbs here, but higher-order functions are amazing. Consider this OCaml library function List.map which applies a function to all elements of the list. It uses recursion to operate on all elements of the list, but takes in an innocuous anonymous function on the surface.
# let doubled_lst = List.map (fun elt -> 2 * elt);;
val doubled_lst : int list -> int list = <fun>
# doubled_lst [2; 3; 4; 5];;
- : int list = [4; 6; 8; 10]
# doubled_lst [0; 2; (-4); 7];;
- : int list = [0; 4; -8; 14]
Functions that adopt and produce functions prevent endangering my fascination for functions. As OCaml’s top-level also says, they are <fun>!
What’s your Type?
I don’t know about all FP languages, but OCaml provides powerful type inference schemes that remove the burden of type definitions on the programmer. All along this post, have you noticed how the OCaml top-level could determine the type of a definition/value? If you haven’t already, take a look at this screenshot from the beginning of this post (Image 2). Notice how the top-level inferred 2 * 4 to be an int with value 8 and x to be of type string.

Not just for these straight-forward instances, but OCaml’s compiler can also decipher types of our instance nble_fst as val nble_fst : int -> int list -> int list and modify_fst as val modify_fst : ('a -> 'a) -> 'a list -> 'a list. In the case of nble_fst, OCaml determines that nble_fst requires an int and an int list (read: a list of ints), and promises to return an int list. The case of modify_lst is a little more complicated, and I won’t go in detail. This could be a brief aid: 'a is polymorphic, meaning that the type of the variable-identifier at that place could be anything; however, the restriction is that the type must be consistent for all 'as appearing in the type expression. Here’s a more detailed analysis on such polymorphic types.
I also won’t go into how OCaml infers those types. But it’s cool. Coupled with merlin in Atom or Visual Studio Code, OCaml infers those types on the go (after adding plugins in Atom and VSCode)! Atom or VSCode can then warn you of type-mismatch errors as the OCaml back-end support infers types on the fly. This is quite different from Java where you would have to define the types of your variables and functions:
// precondition: n >= 0
public static int factorial(int n) {
if (n == 0)
return 1;
else
return n * factorial(n - 1);
}
We have to define that n must be of type int and that factorial(n) returns a value of type int if the precondition is satisfied. No such mess in OCaml:
(* we must write [rec] to tell OCaml that [factorial]
is recursive *)
# let rec factorial = fun n ->
if n = 0 then 1
else n * factorial (n-1);;
val factorial : int -> int = <fun>
The Python variant is:
>>> def factorial(n):
... if n == 0:
... return 1
... else:
... return n * factorial(n - 1)
...
Now you may say, “Hey! Isn’t Python great in this regard then?”. No, not to a large extent.
Since Python embodies dynamic typing (identifying types at runtime), Python code is often error-prone. Whenever I recall how often I have committed the crime of using + to add ints, floats, lists, strings etc., and got a glaring TypeError due to badly-typed code, I introspect how many minutes of my life I would have saved and thus lived longer. Obviously, this is an extreme sentiment, but being aware of the types of values before execution is helpful. The OCaml compiler infers types for you as it compiles and throws errors when you write badly-typed code like this:
# let x = 1 + "hello";;
Error: This expression has type string but an expression was expected of type
int
Although Python doesn’t support static typing out-of-the-box, and its foundations are particularly designed for dynamic typing, type annotations can be of great help. These typing hints are not enforced, but it aids the reader-programmer in figuring out the ins and outs of the code:
>>> from typing import Optional
>>> def add5(n: int) -> Optional[int]:
... if asteroid_crashed_on_earth:
... return None
... else: # all is good on Earth
... return n + 5
...
Optional from the typing module tells me that add5 would either return None or an int. Similarly, n is preferred to be of type int (the Python interpreter can’t natively enforce type checking). With such type annotations, Python looks more like Java and appeals to the programmer’s eyes and mind. Robin Milner won a Turing Award for his work on type inference and ML, one of the early FP languages. There must be some importance of type systems if the CS community bestowed an award on relevant work.
Remember, OCaml knows your type.
Concluding Remarks
Phew. Long post. I still haven’t discussed pattern-matching, type polymorphism, proof assistants, and all the great stuff I learned in CS 3110 at Cornell. I am looking forward to learning more about this side of CS (in my view, it could very well be the light side).
I hope this was a good learning experience for you! I will appreciate any feedback on this post’s content in the comments below.

Resources
Introductory (recommendations before reading this post)
- Danaher, E., “Introduction to OCaml”
- Wikipedia, “Type System”
Intermediate (good for continuing at this level)
- Miles, “Why care about Functional Programming?”.
- Bhargava, A., “Functors, Applicatives, And Monads In Pictures”
Advanced (you got this)
- Zargham M., “Computer Architecture”, “Ch. 2: Von Neumann Architecture”
- Church A., “A Formulation of the Simple Theory of Types”
- Cornell University, Dept. of Computing and Information Sciences, CS 3110 Course